MATHEMATICS:
Sieving Prime Numbers From Thin Ore
Barry Cipra
Mathematicians have known since Euclid that there is
an infinite number of prime numbers. For the last 100 years, they have
even had a good way to determine, approximately, how many primes there
are up to any given number. But the finer points of how primes are
distributed remain, by and large, mysterious. In particular,
mathematicians are almost always unable to take an infinite but
sparsely distributed set of integers, such as the values of n2 + 1, and tell how rich in primes it is.
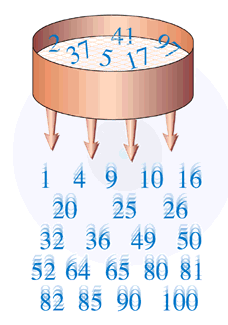Prime cut. The sieve captures the primes in the sequence of numbers of the form
a2 +
b4, up to 100.
ILLUSTRATION: L. CARROLL
That barrier is beginning to yield. In what number theorists are
calling a major breakthrough, two mathematicians have developed
powerful new techniques for assaying such "thin" subsets of integers
for primes. As John Friedlander of the University of Toronto and Henryk
Iwaniec of Rutgers University in New Brunswick, New Jersey, report in a
paper to appear in the Annals of Mathematics,
they have refined a tool known as the asymptotic sieve, developed in
the 1970s by Enrico Bombieri of the Institute for Advanced Study in
Princeton, New Jersey. Their first conquest: a remarkably thin sequence
consisting of numbers of the form a2 + b4.
Friedlander and Iwaniec's new sieve shows that even though most such
numbers are composite--products of prime factors--the sequence includes
an infinite number of primes.
"This is totally new," says Bombieri. The conclusion, he adds, "is what
you would expect from heuristic arguments, but to prove things is
another matter!" In his opinion, Friedlander and Iwaniec have written
"one of the most important papers in analytic number theory of the
century." It "will find a lot of applications" in exploring the
distribution of primes.
Roughly speaking, a mathematical sieve determines the abundance of
primes in a long list of numbers by estimating how many numbers remain
when multiples of small primes are removed--a procedure that sifts out
most composite numbers. For example, of the numbers between 169 and 289
(the squares of the primes 13 and 17), roughly half remain when you
delete the even numbers, two-thirds of those remain after the multiples
of 3 are removed, etc. Sieving the 120 numbers in the sequence yields
an estimate of 120 x (1/2) x (2/3) x (4/5) x (6/7) x (10/11) x (12/13)
= 23 primes. That's close to the exact count, 22. Similar sieves can be
designed for other number sequences. The real work comes in analyzing
the errors in such estimates to get rigorous results.
The errors are easiest to estimate for "dense" sequences such as 1, 5,
9, 13, etc.--a progression that contains roughly one-fourth of all
numbers up to a given size. But Friedlander and Iwaniec's sequence
contains a vanishingly small fraction of the integers. That thinness
makes it impossible to estimate the errors in the usual way, putting
the sequence out of the reach of previous sieves. "Nobody dreamed you
could analyze such sequences," says Bombieri.
The new techniques rely on special algebraic properties of the formula a2 + b4. In a number system known as the Gaussian integers, which enlarges the set of ordinary integers by including i, the square root of -1, such numbers can always be factored as (a + b2i) (a - b2i).
By putting their numbers into this form, Friedlander and Iwaniec were
able to exploit the well-developed theory of algebraic numbers to get a
handle on the errors when they applied their sieve.
The combination of algebraic number theory and sieve techniques is what
Peter Sarnak of Princeton University finds most impressive. "These are
two different worlds, algebra and the sieve," he notes. But because the
technique relies on properties found in only a small fraction of
sequences, many of sieve theory's dearest problems still look hopeless.
In particular, numbers of the form n2
+ 1--1, 2, 5, 10, 17, 26, etc.--almost certainly include an infinite
number of primes; indeed, number theorists have even conjectured an
estimate for how many there are up to any given integer in the
sequence. But no proof appears to be forthcoming. Number theorists are
also convinced that each interval between consecutive squares contains
at least one prime, but have no idea how to prove it.
"The answer to most of these questions is, we don't know," says Andrew
Granville, a number theorist at the University of Georgia in Athens.
"It's frightening how pathetic our knowledge is!"
